Links
Motivation
Boolean minimization remains a practical leverage point in digital design and search‑heavy tooling. The Quine–McCluskey (Q–M) procedure is exact, but naïve dense implementations become memory‑bound well before arithmetic resources are saturated. Our goal is not to change Q–M’s mathematics, but to raise operational intensity by improving spatial and temporal locality.
Baseline
We start from a dense bit‑sliced implementation (DenseQMC): ternary implicants are packed into a 3^n bitset; variables are split into a small bottom layer (h=5) and a top layer (n−5). The algorithm performs top‑merge, bottom merge+reduce, then top‑reduce. This induces many full‑table, high‑stride scans across top dimensions. Once the table exceeds cache, stall time dominates.
Approach (High‑Level)
We restructure execution to complete more related work while data is hot, reduce long strides, and minimize passes:
- CROSS‑DIM — block multiple top dimensions and process a compact 3^t working set before advancing; far fewer long traversals.
- SMOOTHING — generate short kernels for the tail dimensions (t, t−1, …, 1) so each pass remains block‑shaped.
- CROSS‑LAYER — fuse bottom‑layer work with the lowest b top dimensions in one contiguous sweep, eliminating extra global passes.
- MERGE‑SKIP (conservative) — in top‑merge only, omit a redundant lower‑dim triple; keep top‑reduce complete.
- Lean bottom kernels — explicit load→compute→store structure exposes ILP; optional AVX variants are competitive once memory traffic drops.
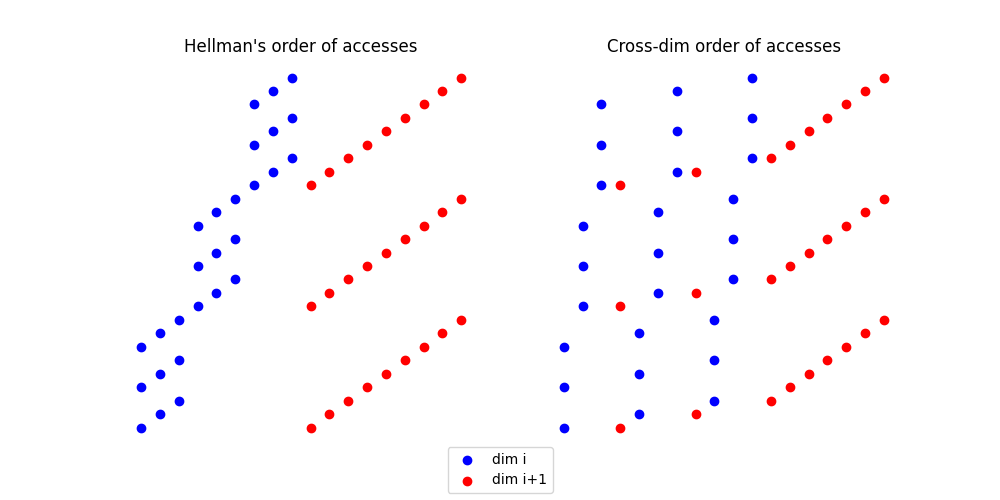
Results (Summary)
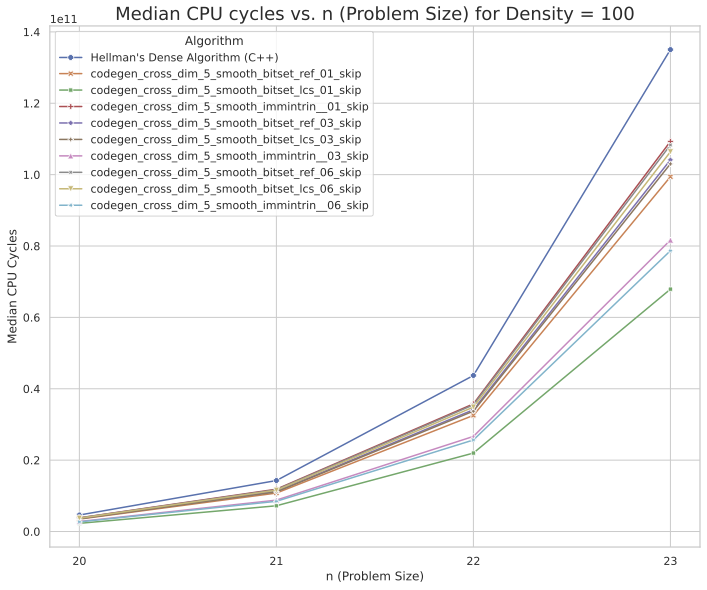
On a Zen‑2 laptop‑class CPU with -O3 -march=native -mavx2, the fused, smoothed, blocked variant delivers ~2.06× speedup at n≈23 relative to DenseQMC. Gains increase with n as the working set crosses L2/L3, reflecting higher locality and fewer full‑table passes.
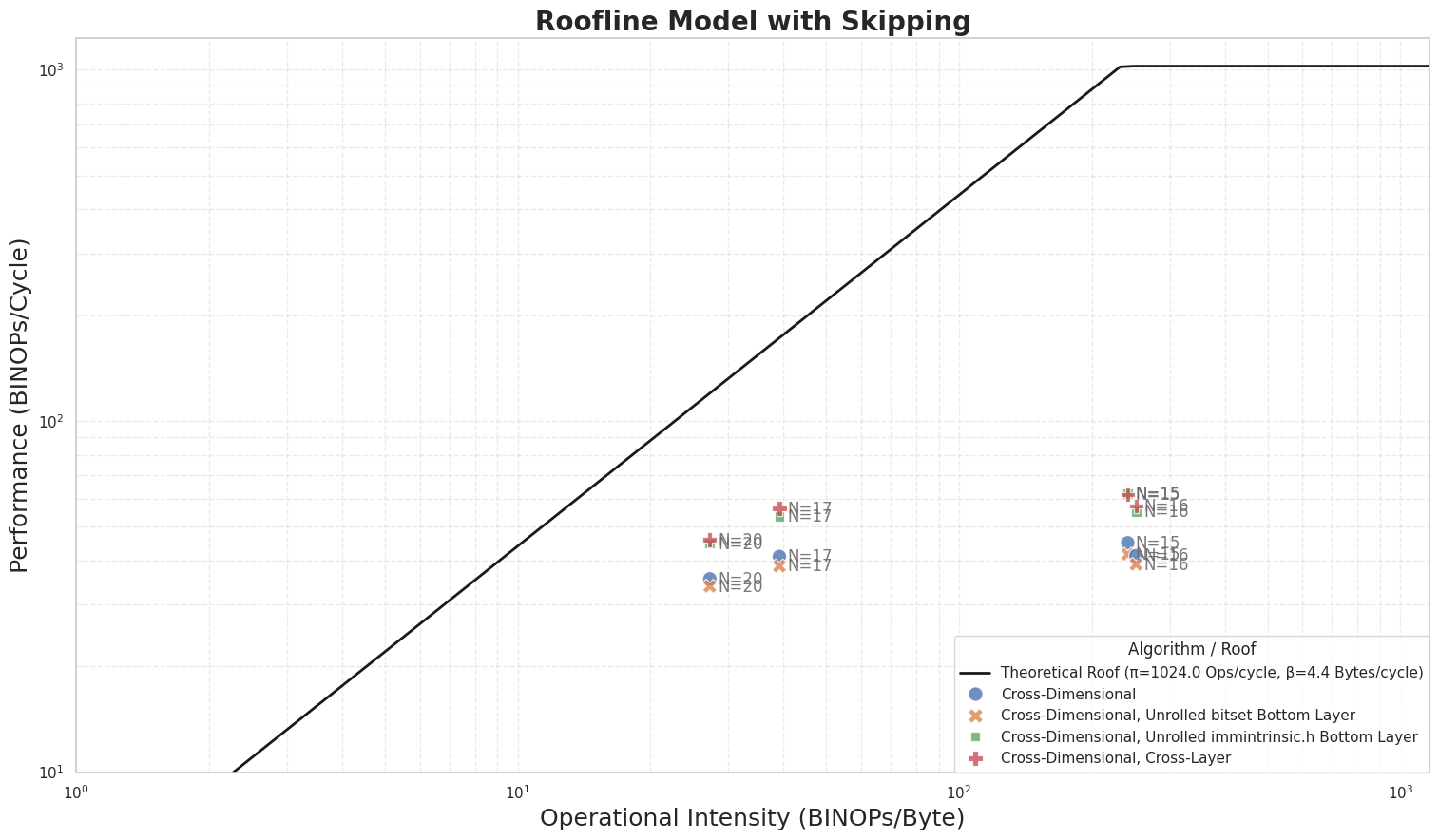
Interpretation
- Blocked/fused schedules shift points rightward on roofline plots (more bytes reused per operation) and climb toward the compute roof for mid‑range n.
- Instruction‑level tweaks matter less than reducing long strides and doing adjacent work together.
