Model-free Approximate RL
Overview
Now we leave the tabular comfort zone. Key aims: reinterpret TD/Q updates as stochastic optimization, understand why deep Q-learning needs stabilizers, tame policy gradient variance, and see how entropy-regularized RL links back to probabilistic inference.
TD/Q as stochastic optimization
- Parametrize value/Q with \(\theta\) and fit the Bellman equation in least-squares form.
- Per-sample TD loss: \(\ell(\theta)=\tfrac{1}{2}\big(r+\gamma V(x';\theta^-) - V(x;\theta)\big)^2\) with target network \(\theta^-\) frozen for stability; gradient \(\nabla_\theta \ell = (V(x;\theta)-y)\nabla_\theta V(x;\theta)\).
- Function approximation + bootstrapping + off-policy = “deadly triad” ⇒ convergence no longer guaranteed, so we need heuristics (replay buffers, target networks, clipping, etc.).
Deep Q-Network (DQN) family
- Replay buffer \(\mathcal{D}\) makes samples approximately IID.
- Target network updates every \(K\) steps.
- Loss: \(\mathcal{L}_{\mathrm{DQN}}=\tfrac{1}{2}\mathbb{E}_{(x,a,r,x')\sim\mathcal{D}}\big[r+\gamma\max_{a'}Q(x',a';\theta^{-})-Q(x,a;\theta)\big]^2\).
- Maximization bias: \(\max\) of noisy estimates overestimates true values. Double DQN fixes this via decoupled action selection/evaluation: target \(r + \gamma Q(x',\arg\max_{a'}Q(x',a';\theta);\theta^{-})\); side-by-side sweep below shows the over-optimism gap.
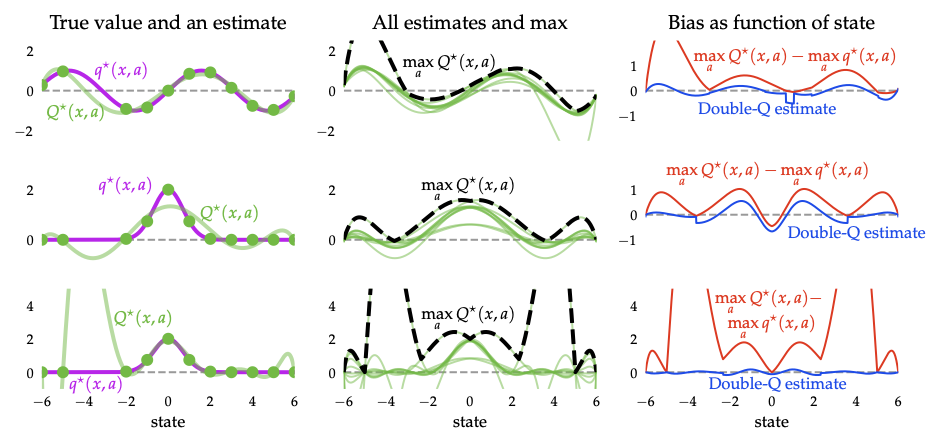
- Companion tricks: dueling networks, prioritized replay, distributional RL, noisy nets — all to stabilize training or encourage exploration.
Vanilla policy gradients (REINFORCE)
- Objective \(J(\varphi)=\mathbb{E}_{\tau\sim\pi_\varphi}\big[\sum_{t\ge0}\gamma^t r_t\big]\).
- Score-function gradient (Lemma 12.5): \(\nabla_{\varphi}J = \mathbb{E}_{\tau}\big[\sum_{t} \gamma^t G_{t:T}\,\nabla_{\varphi}\log\pi_{\varphi}(a_t\mid s_t)\big]\).
- Baselines (Lemma 12.6): subtract \(b_t\) independent of \(a_t\) (state-dependent baselines yield downstream returns form) to cut variance.
- REINFORCE (Alg. 12.2): Monte Carlo gradient ascent; unbiased but high variance, sensitive to learning-rate choice and can stall in local optima.
On-policy actor-critic family
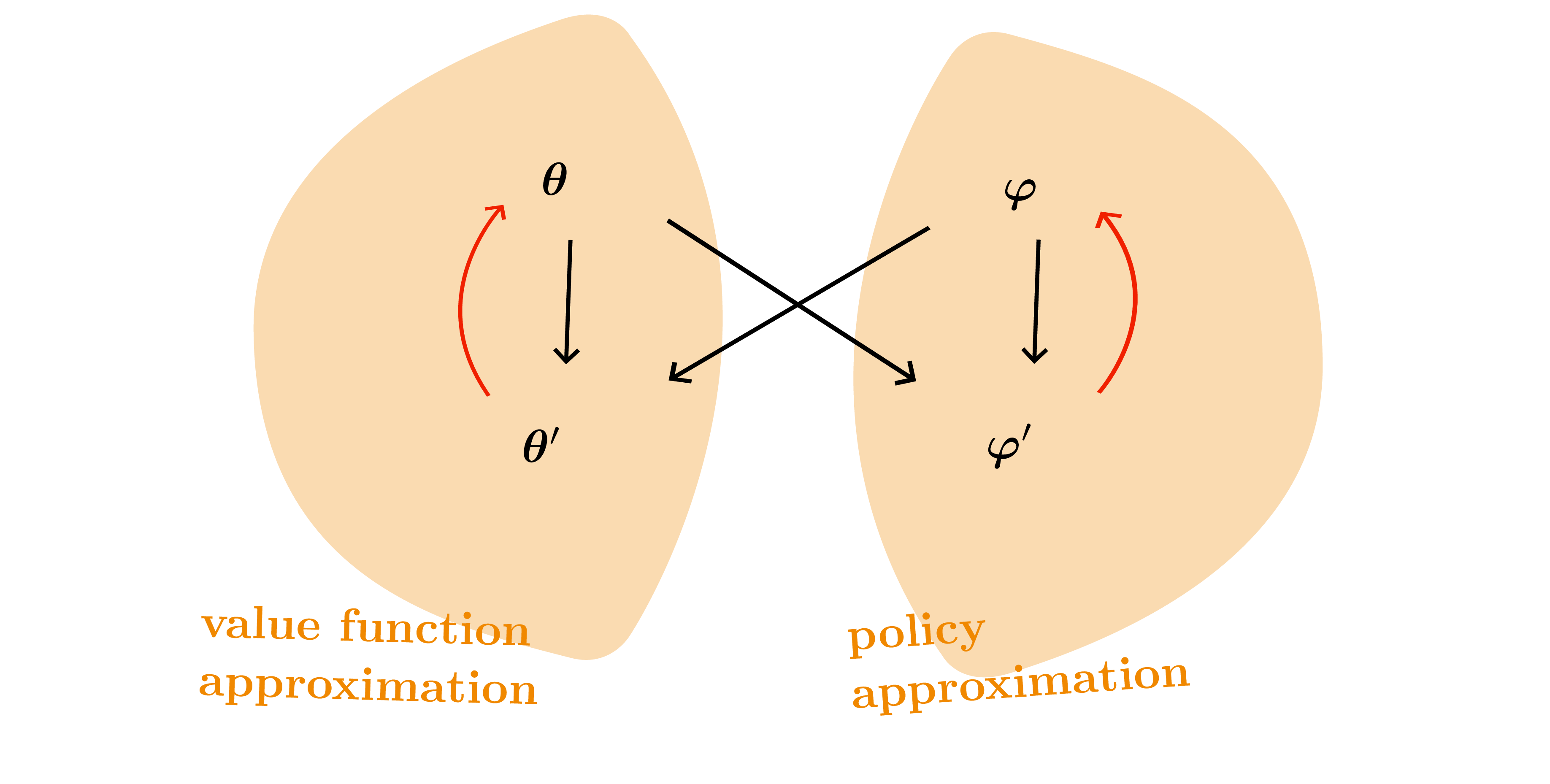
- Actor = policy \(\pi_{\varphi}\), critic = value/Q \(\hat{Q}_{\theta}\).
- Online actor-critic (Alg. 12.3): update actor with \(\hat{Q}_{\theta}\) and critic with SARSA-style TD errors.
- Advantage Actor-Critic (A2C): \(\hat{A}_t=r_t+\gamma V(s_{t+1})-V(s_t)\) reduces variance.
- Generalized Advantage Estimation (GAE): \(\hat{A}^{\mathrm{GAE}(\lambda)}_t = \sum_{k\ge0}(\gamma\lambda)^k\delta_{t+k}\) with TD errors \(\delta_t=r_t+\gamma V(s_{t+1})-V(s_t)\); tunable bias/variance.
- Policy gradient theorem (Eq. 12.24): \(\nabla_{\varphi}J = \frac{1}{1-\gamma}\mathbb{E}_{s\sim\rho_{\pi},a\sim\pi}[A^{\pi}(s,a)\nabla_{\varphi}\log\pi_{\varphi}(a\mid s)]\).
- Trust-region methods: TRPO maximizes surrogate under KL constraint; PPO simplifies via clipping or KL penalty; GRPO removes critic using group-relative baselines.
Off-policy actor-critics
- Deterministic Policy Gradient (DPG/DDPG): critic trained like DQN, actor updated via \(\nabla_a Q(s,a)\); requires exploration noise.
- Twin Delayed DDPG (TD3): twin critics, target policy smoothing, delayed actor updates reduce overestimation.
- Stochastic Value Gradients (SVG): use reparameterization for stochastic policies \(a=g(\varepsilon; s,\varphi)\).
Maximum-entropy RL and SAC
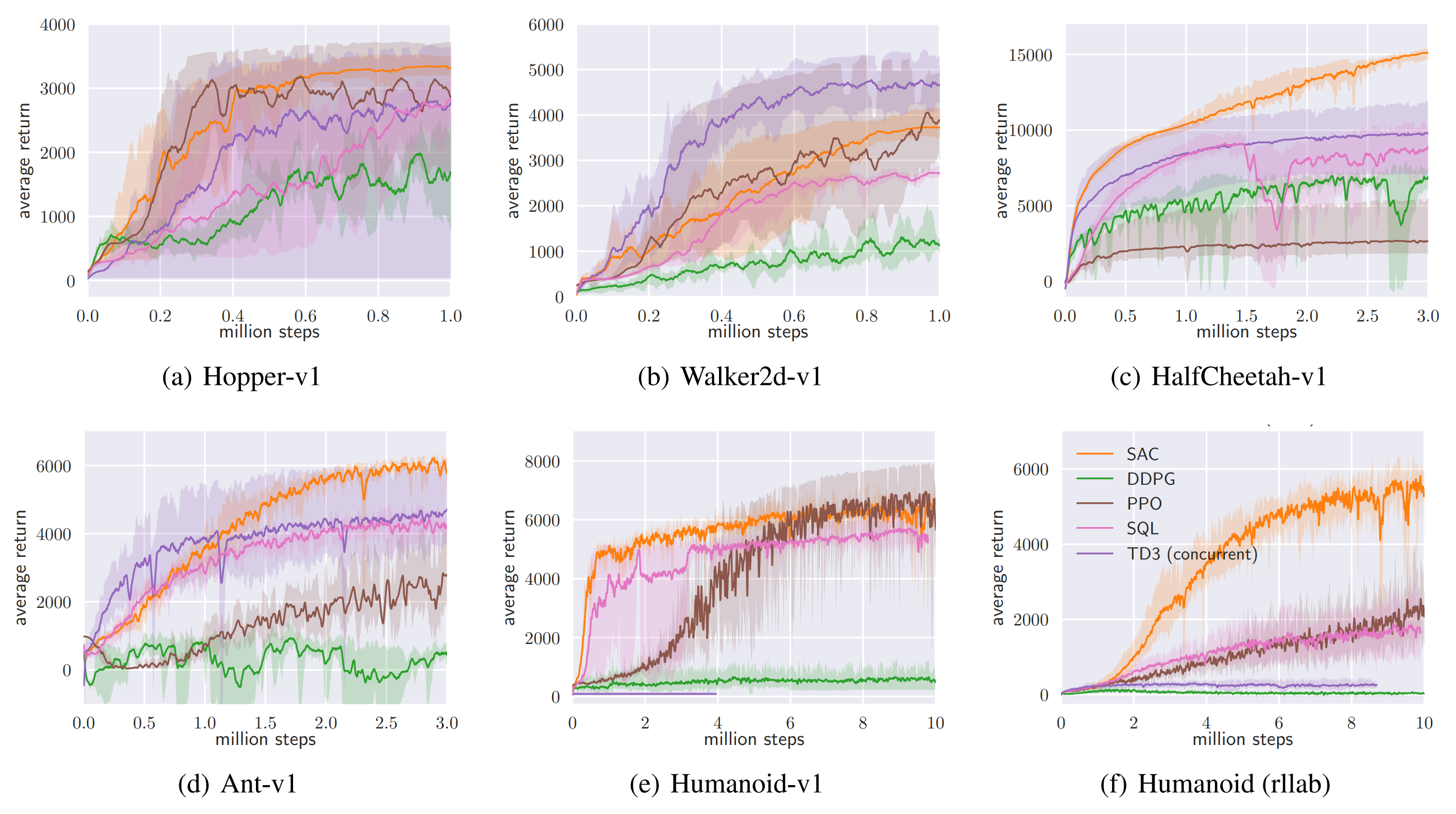
- Soft objective \(J_{\alpha}(\pi)=\mathbb{E}[\sum_t\gamma^t(r_t+\alpha\mathcal{H}(\pi(\cdot\mid s_t)))]\).
- Soft Bellman backups: \(Q(s,a)=r+\gamma\mathbb{E}_{s'}[V(s')]\), \(V(s)=\alpha\log\int \exp(Q(s,a)/\alpha)da\).
- Soft Actor-Critic (SAC): off-policy, stochastic actor; critic matches soft Q, actor minimizes KL to Boltzmann \(\propto\exp((Q-\alpha\log\pi)/\alpha)\); temperature \(\alpha\) tuned to target entropy.
- Provides intrinsic exploration and strong sample efficiency in continuous control; entropy plot below shows how higher temperature flattens the implied policy.
Preference-based RL & large models
- RLHF/RLAIF pipeline: supervised fine-tune baseline model, learn reward model from preferences, optimize policy via PPO/GRPO with KL penalty to reference.
- Objective \(\mathbb{E}[r_{\text{RM}}(y) - \beta\,\mathrm{KL}(\pi\|\pi_{\text{ref}})]\) ↔︎ probabilistic inference with KL regularization.
- Critical for aligning large language models; relies on PPO/GRPO mechanics described above.
Practical heuristics & cross-links
- Replay + target networks come from DQN and power DDPG/TD3/SAC.
- Advantage baselines (A2C/GAE) inherit variance-reduction lemmas from variational inference.
- Trust-region/clipping echo KL-constrained optimization in VI.
- Entropy bonuses tie back to max-entropy active learning and variational inference.
Every deep RL algorithm is some combination of: replay, target networks, advantage estimates, trust-region regularization, and entropy bonuses. Keep these primitives handy.