Active Learning

Overview

Turn posterior uncertainty into data-acquisition policies. Mutual information + submodularity justify greedy sampling.

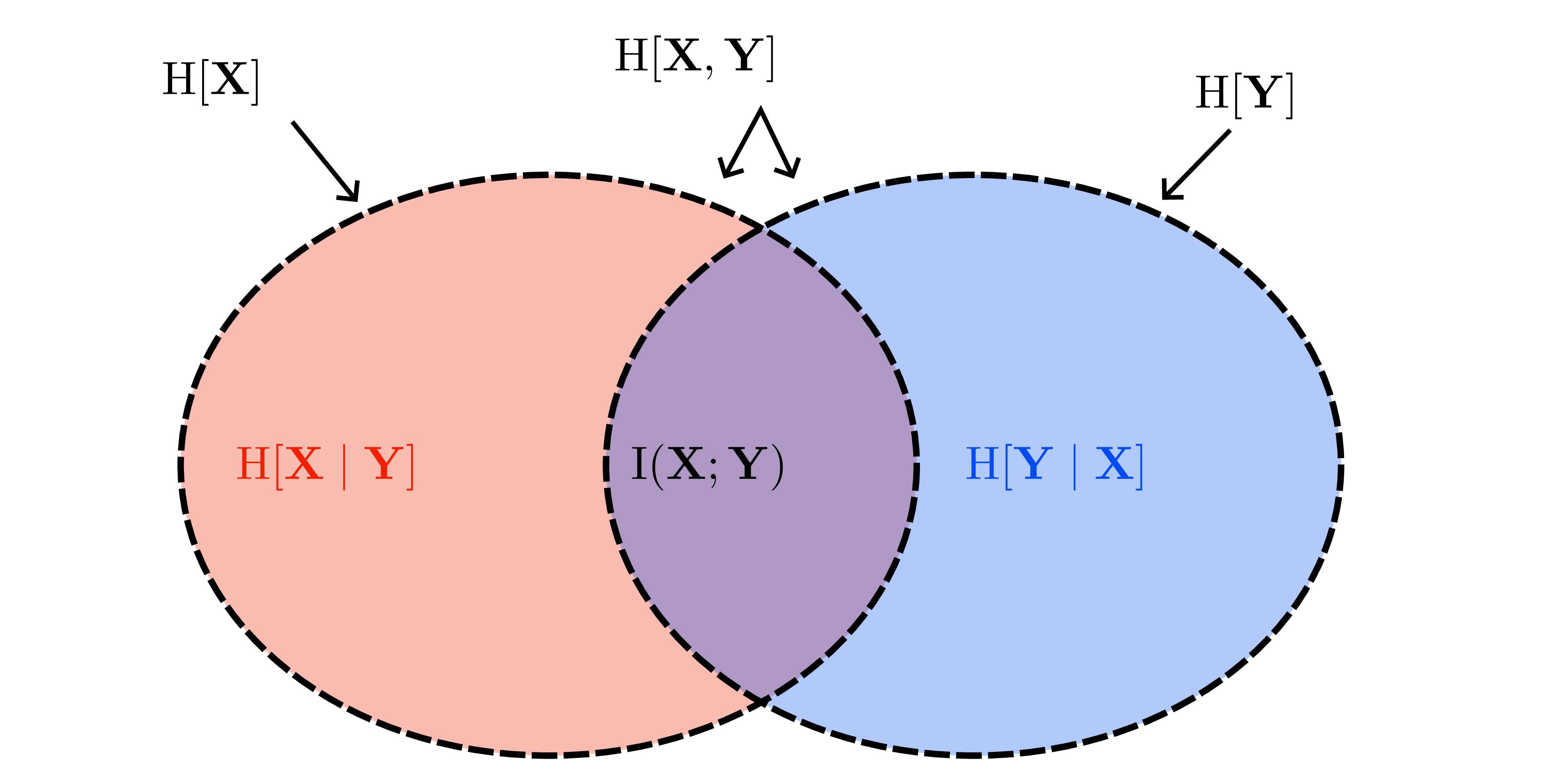
Figure 1: Mutual information decomposed as overlapping entropy of \(X\) and \(Y\).

Entropy and mutual information recap

  • Conditional entropy \(H(X\mid Y)=\mathbb{E}[-\log p(X\mid Y)]\) measures expected residual uncertainty after observing \(Y\); “information never hurts”: \(H(X\mid Y)\le H(X)\).
  • Mutual information \(I(X;Y)=H(X)-H(X\mid Y)=H(Y)-H(Y\mid X)\) quantifies expected entropy reduction.
  • Conditional MI \(I(X;Y\mid Z)\) supports incremental updates; interaction information distinguishes redundancy vs synergy.
  • Data processing inequality: \(X\to Y\to Z\) ⇒ \(I(X;Z)\le I(X;Y)\) — ensures that coarsening observations cannot increase utility.

MI-based acquisition

  • Observations \(y_x = f(x) + \varepsilon_x\), \(\varepsilon_x\sim\mathcal{N}(0,\sigma_n^2)\).
  • Utility of subset \(S\subseteq\mathcal{X}\): \[I(S)=I(f_S; y_S) = H(f_S) - H(f_S\mid y_S).\]
  • Marginal gain when adding \(x\): \[\Delta_I(x\mid S) = I(f_x; y_x\mid y_S) = H(y_x\mid y_S) - H(\varepsilon_x).\] First term = posterior predictive entropy at \(x\), second = irreducible noise.
  • For Gaussian models (e.g., GP surrogate) \(H(y_x\mid y_S)\) has closed form via posterior variance.

Submodularity & greedy optimality

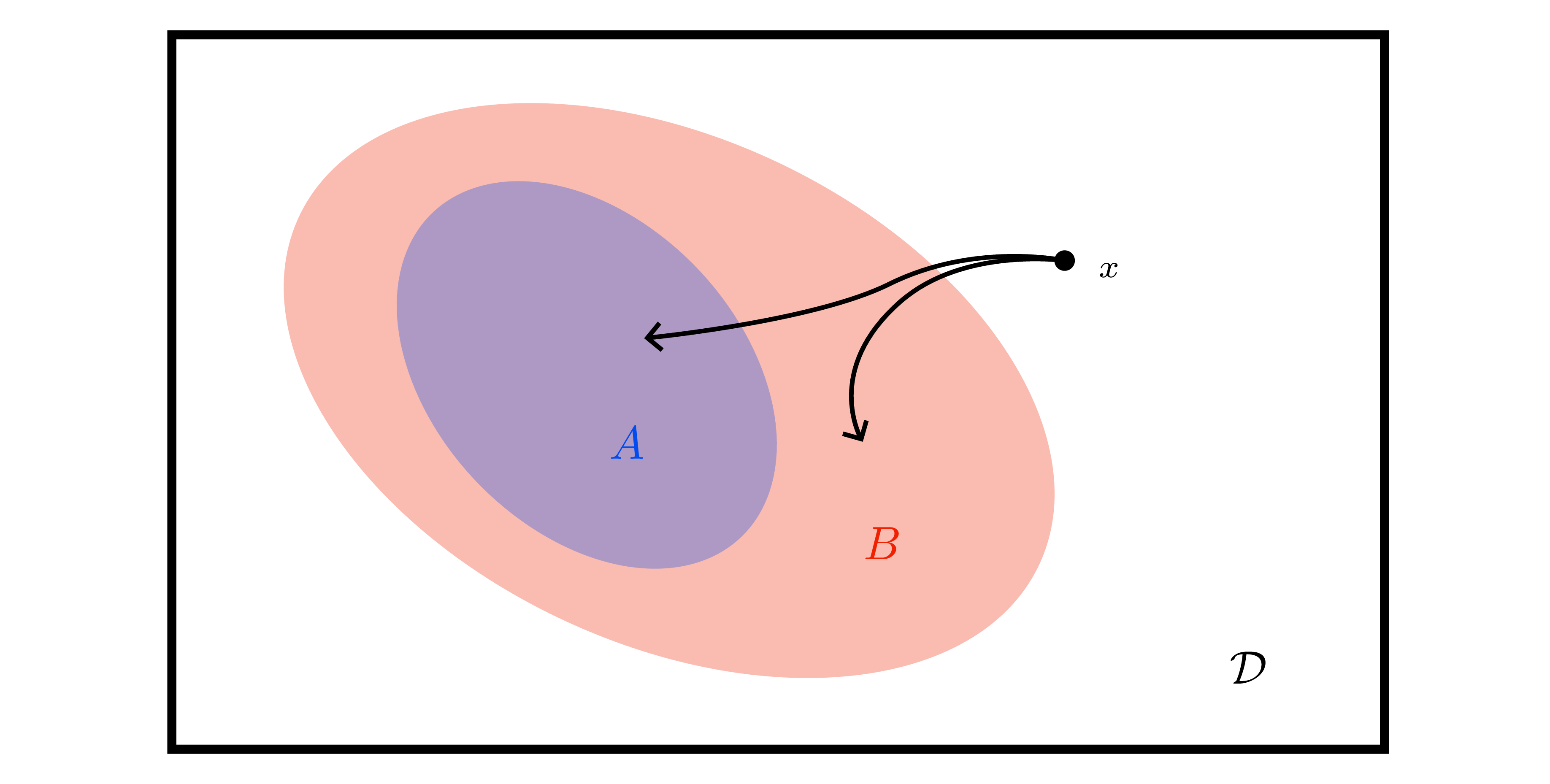
Figure 2: Monotone submodularity. The effect of adding \(x\) to the smaller set \(A\) is larger than the effect of adding \(x\) to the larger set \(B\).
  • Function \(F\) is submodular if \(\Delta_F(x\mid A) \ge \Delta_F(x\mid B)\) whenever \(A\subseteq B\) — discrete analogue of concavity.
  • Mutual information \(I(S)\) is monotone submodular when observations are conditionally independent given latent \(f\) (true for GP with Gaussian noise, LVMs, etc.). Ergo greedy selection (Argmax of \(\Delta_I\)) is \((1-1/e)\)-approximate optimal (Nemhauser et al.).
  • Absence of synergy corresponds to submodularity (Exercise 8.3): if learning one point never increases the value of another, greedy works.

Greedy active learning loop

  1. Maintain posterior over \(f\) (GP or Bayesian NN).
  2. For each candidate \(x\), compute predictive entropy \(H(y_x\mid y_S)\) and marginal gain \(\Delta_I(x\mid S)\).
  3. Select \(x^{\star}=\arg\max_x \Delta_I(x\mid S)\) (or pick \(k\) highest for batch selection).
  4. Query label, update posterior, repeat until budget exhausted.

Variants & practical notes

  • Batch active learning: use submodular maximization with lazy evaluation or approximate greedy.
  • Diversity heuristics: when posterior approximations cheap, combine MI with coverage or kernel herding.
  • Non-Gaussian likelihoods: use MC estimates of entropy/MI (requires VI or Laplace approximations for tractable gradients).
  • Noisy annotation costs: weigh MI by cost or expected improvement per time.

Active learning is curiosity formalized: reduce epistemic uncertainty fastest while respecting label budgets. The same MI machinery powers Bayesian optimization and model-based RL exploration bonuses.