Gaussian Processes

Overview

Infinite-dimensional generalization of Bayesian linear regression. Kernels encode function priors; posterior algebra mirrors BLR but now happens in function space.

Figure 1: Bayesian optimization loop: observe \(y_t = f(x_t) + \varepsilon_t\) after querying \(x_t\).

Definition

  • A Gaussian process \(f\sim\mathcal{GP}(\mu,k)\) assigns to every finite index set \(\mathcal{A}=\{x_1,\dots,x_m\}\) a joint Gaussian \(\mathbf{f}_{\mathcal{A}}\sim\mathcal{N}(\mu_{\mathcal{A}},K_{\mathcal{A}\mathcal{A}})\) with \((K_{\mathcal{A}\mathcal{A}})_{ij}=k(x_i,x_j)\).
  • Observation model: \(y_i=f(x_i)+\varepsilon_i\), \(\varepsilon_i\sim\mathcal{N}(0,\sigma_n^2)\) independent.
  • Prior predictive at \(x\): \(y\mid x\sim\mathcal{N}(\mu(x), k(x,x)+\sigma_n^2)\).
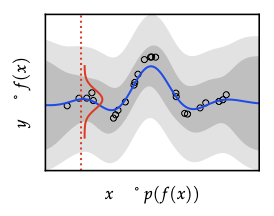
Figure 2: Gaussian processes behave like infinite-dimensional Gaussians: blue mean function with dark (epistemic) and light (aleatoric) uncertainty bands.

Posterior conditioning (same algebra as BLR)

Given training data \((\mathbf{X},\mathbf{y})\), define \(K=K_{\mathbf{X}\mathbf{X}}\) and \(k_x = k(x,\mathbf{X})\). Posterior is \[ f\mid\mathcal{D} \sim \mathcal{GP}(\mu',k'), \] with \[ \mu'(x)=\mu(x)+k_x^{\top}(K+\sigma_n^2 I)^{-1}(\mathbf{y}-\mu_{\mathbf{X}}), \] \[ k'(x,x')=k(x,x')-k_x^{\top}(K+\sigma_n^2 I)^{-1}k_{x'}. \] Predictive label variance adds \(\sigma_n^2\) back in. Conditioning always reduces covariance (Schur complement PSD).

Sampling

  • Direct: draw \(\xi\sim\mathcal{N}(0,I)\) and compute \(f=\mu + L\xi\) with \(L\) Cholesky of \(K\) (\(\mathcal{O}(n^3)\)).
  • Forward sampling: generate points sequentially using conditional Gaussians (same complexity but conceptually useful for illustration).

Kernels

  • Valid kernel iff Gram matrix PSD for any finite set; closure under sum/product/positive scaling/polynomials/\(\exp\).
  • Stationary \(k(x,x')=\tilde{k}(x-x')\); isotropic depends only on \(\|x-x'\|\).
  • Important families:
    • Linear \(k(x,x')=\sigma_p^2 x^\top x'\) ↔︎ BLR.
    • Squared exponential (RBF) \(\exp(-\|x-x'\|^2/(2\ell^2))\) → infinitely smooth.
    • Matérn \((\nu,\ell)\) controls differentiability (# of mean-square derivatives \(=\lfloor\nu\rfloor\)); Laplace is Matérn \(\nu=1/2\).
    • Periodic, rational quadratic, ARD kernels for anisotropy.
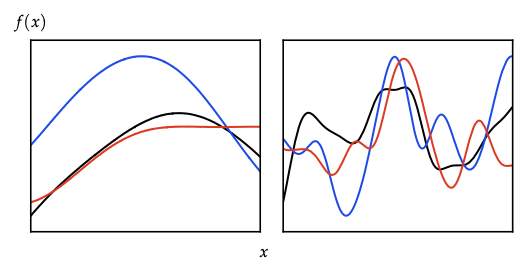
Figure 3: Functions sampled from an RBF kernel GP with length scales \(h=5\) (left) and \(h=1\) (right).
  • Feature-space story: \(k(x,x')=\phi(x)^\top\phi(x')\) (Mercer). Random Fourier features approximate stationary kernels via Bochner.

Hyperparameter selection

  • Marginal likelihood \(p(\mathbf{y}\mid\mathbf{X},\theta)=\mathcal{N}(0,K_{\theta}+\sigma_n^2 I)\).
  • Log-evidence (Eq. 4.18) balances data fit \(\mathbf{y}^\top K^{-1}\mathbf{y}\) vs complexity \(\log|K|\).
  • Optimize wrt kernel parameters (\(\ell\), signal variance, noise) via gradient-based methods; derivatives involve trace identities.
  • Bayesian treatment: put priors on hyperparameters and integrate (costly; approximations via HMC/VI possible).

Scalability / approximations

  • Exact cost \(\mathcal{O}(n^3)\) ⇒ approximations needed for large \(n\).
  • Local/sparse methods: inducing points (FITC, VFE), Nyström approximations, structured kernel interpolation.
  • Feature approximations: random Fourier features (stationary kernels), orthogonal random features, sketching.
  • Kron/Toeplitz exploitation for grid inputs.

Connections forward

  • GP posterior mean = kernel ridge regression estimate; posterior variance drives exploration bonuses and safety analysis.
  • Evidence maximization parallels empirical Bayes in BLR and hyperparameter tuning in Bayesian neural nets.
  • Kernels express prior assumptions; in Bayesian optimization they define smoothness and drive acquisition functions.