Fundamentals of Inference

Overview

Bedrock for everything else: probability spaces, conditioning, and information measures. Later chapters reuse these definitions verbatim.

Figure 1: Conditioning an event \(A\) on another event \(B\) can be understood as replacing the universe of all possible outcomes \(\Omega\) by the observed outcomes \(B\). Then, the conditional probability is simply expressing the likelihood of \(A\) given that \(B\) occurred.

Probability spaces and viewpoints

  • Probability space \((\Omega,\mathcal{A},\mathbb{P})\): outcome space, \(\sigma\)-algebra, and measure with \(\mathbb{P}(\Omega)=1\); Borel \(\sigma\)-algebra for \(\mathbb{R}^d\).
  • Frequentist view: \(\Pr[A]=\lim_{N\to\infty}\frac{1}{N}\sum_{i=1}^N\mathbf{1}\{A\text{ occurs in trial }i\}\) when IID replicates exist.
  • Bayesian view: \(\Pr[A]\) encodes coherent belief; Dutch-book coherence ⇒ Kolmogorov axioms. Prior/posterior updates by Bayes’ rule.

Random variables and transformations

  • Measurable map \(X:(\Omega,\mathcal{A})\to(\mathcal{X},\mathcal{B})\) pushes forward \(\mathbb{P}\) to \(P_X\).
  • Discrete: PMF \(p_X(x)=\Pr[X=x]\), CDF \(F_X(x)=\Pr[X\le x]\).
  • Continuous: PDF \(p_X\) with \(\Pr[X\in S]=\int_S p_X(x)\,dx\).
  • Support \(\text{supp}(p)=\{x:p(x)>0\}\) is crucial for conditioning (e.g., KL terms later).
  • Change of variables: for invertible \(g\) with Jacobian \(J\), \(p_Y(y)=p_X(g^{-1}(y))\left|\det J_{g^{-1}}(y)\right|\).

Conditioning identities

  • Product rule: \(\Pr[A,B]=\Pr[A\mid B]\Pr[B]\).
  • Law of total probability: \(\Pr[A]=\sum_i\Pr[A\mid B_i]\Pr[B_i]\) or \(\int \Pr[A\mid b]p_B(b)db\).
  • Bayes’ rule: \(\Pr[B\mid A]=\frac{\Pr[A\mid B]\Pr[B]}{\Pr[A]}\); density form \(p_{X\mid Y}(x\mid y)=p_{X,Y}(x,y)/p_Y(y)\).
  • Tower property: \(\mathbb{E}[X]=\mathbb{E}_Y[\mathbb{E}[X\mid Y]]\); used repeatedly in variance decompositions and TD learning.

Expectations, variance, covariance

  • Expectation linear; Jensen: convex \(g\) ⇒ \(g(\mathbb{E}[X])\le\mathbb{E}[g(X)]\) (applied in KL bounds, ELBO derivations).
  • Variance: \(\operatorname{Var}[X]=\mathbb{E}[X^2]-\mathbb{E}[X]^2\); covariance matrix \(\Sigma_X=\mathbb{E}[(X-\mathbb{E}X)(X-\mathbb{E}X)^\top]\) PSD.
  • Linear maps: \(\operatorname{Var}[AX+b]=A\operatorname{Var}[X]A^\top\); Schur complement yields conditional covariance (used in GP conditioning, Kalman filters).
  • Law of total variance: \(\operatorname{Var}[X]=\mathbb{E}_Y[\operatorname{Var}[X\mid Y]]+\operatorname{Var}_Y(\mathbb{E}[X\mid Y])\) ⇒ interprets aleatoric vs epistemic uncertainty.

Independence notions

  • \(X\perp Y\) iff joint factorizes; conditional independence \(X\perp Y\mid Z\) iff \(p(x,y\mid z)=p(x\mid z)p(y\mid z)\).
  • Pairwise independence ≠ mutual independence; counterexamples show up in mixture models.
  • Gaussian special case: zero covariance ⇔ independence.

Multivariate Gaussian essentials

  • PDF: \(\mathcal{N}(x\mid\mu,\Sigma)\) with determinant and quadratic form.
  • Affine invariance: \(AX+b\sim\mathcal{N}(A\mu+b, A\Sigma A^\top)\).
  • Sampling: \(x=\mu+L\xi\), \(\xi\sim\mathcal{N}(0,I)\) (Cholesky or spectral) — reused for GP sampling, latent variable models.
  • Conditioning on block partitions: \[X_A\mid X_B=b \sim \mathcal{N}(\mu_A + \Sigma_{AB}\Sigma_{BB}^{-1}(b-\mu_B),\; \Sigma_{AA}-\Sigma_{AB}\Sigma_{BB}^{-1}\Sigma_{BA}).\] Schur complement PSD ⇒ conditioning never increases variance (core to GP posterior, Kalman updates).

Parameter estimation summary

  • Likelihood \(p(\mathcal{D}\mid\theta)=\prod_i p(y_i\mid x_i,\theta)\); MLE solves \(\max_\theta \ell(\theta)=\sum_i \log p(y_i\mid x_i,\theta)\).
  • MAP adds prior \(\log p(\theta)\); recovers ridge/lasso when using quadratic penalties.
  • Bayesian predictive: \(p(y^*\mid x^*,\mathcal{D})=\int p(y^*\mid x^*,\theta)p(\theta\mid\mathcal{D})d\theta\); motivates maintaining posterior rather than point estimates.

Information-theoretic quantities

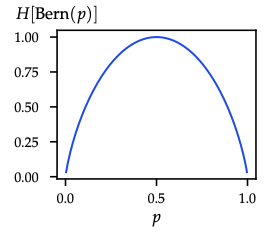
Figure 2: Probability space (left) and the corresponding surprise space obtained via the \(-\log\) transform.
Figure 3: Entropy of a Bernoulli experiment as a function of the success probability \(p\).
  • Surprise \(\mathcal{S}(u)=-\log u\); entropy \(H(p)=\mathbb{E}_p[-\log p(X)]\) measures average surprise.
  • Cross-entropy \(H(p,q)=\mathbb{E}_p[-\log q(X)]\).
  • KL divergence \(\mathrm{KL}(p\|q)=\mathbb{E}_p\big[\log\frac{p}{q}\big]\ge0\); forward KL is mode-covering, reverse KL is mode-seeking.
  • Mutual information \(I(X;Y)=H(X)-H(X\mid Y)\) underlies active learning, Bayesian optimization, and exploration bonuses.

Keep this sheet handy: every later derivation (Bayesian linear regression, VI, Kalman filtering, GP conditioning, RL entropy bonuses) is a remix of these identities.