Machine Learning on Sequential Data

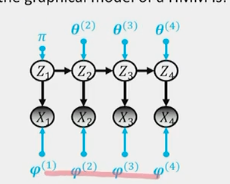
Introduction

Sequential data is a common modality of data. It includes time series, text, and audio. In this post, we will discuss various machine learning models that are used to model sequential data.

Autoregressive Models (AR Models)

Overview

An autoregressive (AR) model is used for modeling and predicting time series data where observations are dependent on previous time steps. Here are the key concepts and components of AR models:

Key Concepts

• Sequence of Observations: \(X_1, X_t\), where \(t\) is a time index, location, etc.
• Continuous Observations: Occur at discrete time steps.
• Applications:
  • Time series forecasting (e.g., temperature, stock prices).
  • Sequence of words in a sentence.
• Dependence: Observations are not independent and identically distributed (not i.i.d.).

AR Model of Order \(p\)

The AR model of order \(p\) is defined as: \[ X_t = c + \sum_{i=1}^{p} \phi_i X_{t-i} + \epsilon_t \] where: - \(\phi_i\) are the parameters of the model. - \(c\) is a constant. - \(\epsilon_t\) is the error term (white noise). - \(X_{t-i}\) is the lagged value of the time series.

Intuitively, the AR model is a linear regression of the current value of the time series on the past \(p\) values.

Long-term Effects

A modification or shock to \(X_t\) will have a long-term effect on the time series.

Regression View

For regression, we can represent the data in matrix form: \[ X = \begin{bmatrix} X_{p-1} & X_{p-2} & \cdots & X_0 \\ X_p & X_{p-1} & \cdots & X_1 \\ X_{p+1} & X_p & \cdots & X_2 \\ \end{bmatrix} \] \[ y = \begin{bmatrix} X_p \\ X_{p+1} \\ X_{p+2} \\ \end{bmatrix} \] The parameters \(\phi\) can be estimated using: \[ \phi = (X^T X)^{-1} X^T y \] or using stochastic gradient descent (SGD) with mean squared error (MSE) loss.

Training

Only one time series is needed to train the model.

Probabilistic View

The probability of \(X_t\) given the past \(p\) values is: \[ P(X_t | X_{t-1}, X_{t-2}, \ldots, X_{t-p}) = \mathcal{N}\left(c + \sum_{i=1}^{p} \phi_i X_{t-i}, \sigma^2\right) \] where: - \(\mathcal{N}\) is the normal distribution. - \(c\) and \(\phi\) are shared across all time steps. - Maximum likelihood estimation (MLE) would be the same as the regression view.

Generative Model

The AR model is also a generative model.

Mean Function

\[ \mu(t) = \mathbb{E}(X_t) \]

Auto Covariance Function

\[ \gamma(t, i) = \mathbb{E}[(X_t - \mu(t))(X_{t-i} - \mu(t-i))] = \text{Cov}(X_t, X_{t-i}) \] - Indicates the dependence between two time steps. - Prediction is not deterministic due to the white noise term.

General Remark: Data Split

• Non-i.i.d Data: We cannot split the data randomly.
• Temporal Split: The model should be trained on past data and tested on future data.
• K-Fold Across Time: Keep the validation set the same size and shift it to the right.

General Remark: Stationarity

A time series is stationary if: - \(\mathbb{E}(X_t) = \mu\) for all \(t\). - \(\text{Cov}(X_t, X_{t-i}) = \gamma(i)\) for all \(t\).

This allows us to estimate \(\mu\) and \(\gamma\) from the data, making it a good modeling assumption.

Parameters

Parameters learned from one part of the time series can be used to predict another part.

Yule-Walker Equations

Assuming stationarity, we can learn the parameters of the AR model using the Yule-Walker equations: \[ \gamma_i = \sum_{t=1}^{p} \phi_t \gamma_{i-t} \] \[ \gamma_0 = \sigma^2 + \sum_{i=1}^{p} \phi_i \gamma(i) \]

• Estimate the moments \(\gamma(i)\) from the data.
• Solve this system of linear equations to get the \(\phi\) parameters.
• Use \(\gamma(0)\) to estimate \(c\) and \(\sigma^2\).

Moment Matching

We use moment matching to estimate parameters.

Questions

Screenshot of questions

Markov Chains

A Markov Chain is a sequence of random variables \(X_1, X_2, \ldots, X_t\) that fulfills the Markov property: \[ P(X_{t+1} \mid X_t, X_{t-1}, \ldots, X_1) = P(X_{t+1} \mid X_t) \]

Discrete Values

• The time indices are discrete.
• The variables \(X_t\) are discrete.

Joint Distribution

The joint distribution is given by: \[ P(X_1, X_2, \ldots, X_t) = P(X_1) P(X_2 \mid X_1) P(X_3 \mid X_2) \ldots P(X_t \mid X_{t-1}) \]

General Distribution

In general, the distribution for each random variable can be different: \[ P(x_1 = i) = \pi_i \] \[ P(X_{t+1} = j \mid X_t = i) = P_{ij}^{t+1} \] where \(\pi \in \mathbb{R}^k\) is the initial distribution and \(P_{ij}^t\) is a \(K \times K\) matrix.

Joint Distribution Simplified

The joint distribution can be expressed as: \[ P(X_1, X_2, \ldots, X_t) = \pi_1 P_1^t P_2^t \ldots P_t^t \] The number of parameters required is \(K(K-1)(t-1) + K-1\), which is too many for large \(t\).

Stationarity

For a stationary process: \[ P(X_{t+1} = j \mid X_t = i) = P_{ij} \] The transition matrix remains the same for all \(t\) (Time Homogeneity).

The number of parameters required is \(K(K-1) + K-1\).

Interpretation

A time-homogeneous discrete Markov Chain can be interpreted as a state machine or a graph.

Learning

Maximum Likelihood Estimation (MLE)

• For \(n\) independent sequences: \[ P(\text{all}) = \prod_{n=1}^{N} P(X_1^n) \prod_{t=1}^{T} P(X_{t+1}^n \mid X_t^n) = \prod_{n=1}^{N} \prod_{i=1}^{K} \pi_i^{L(i)} \prod_{i=1}^{K} \prod_{j=1}^{K} P_{ij}^{L(i,j)} \]
• Where:
  • \(L(i) = \sum_{n=1}^{N} 1(X_1^n = i)\)
  • \(L(i,j) = \sum_{n=1}^{N} \sum_{t=1}^{T-1} 1(X_t^n = i, X_{t+1}^n = j)\)

Log-Likelihood

\[ \log(P(\text{all})) = \sum_{i=1}^{K} L(i) \log(\pi_i) + \sum_{i=1}^{K} \sum_{j=1}^{K} L(i,j) \log(P_{ij}) \]

Maximizing with constraints: - \(\sum \pi_i = 1\) - \(\sum_j P_{ij} = 1\)

Transition Probabilities

\[ A_{ij} = \frac{L(i,j)}{\sum_{j=1}^{K} L(i,j)} \] \[ \pi_i = \frac{L(i)}{\sum_{i=1}^{K} L(i)} \]

\(n\)-Step Transition Probabilities

\[ A_{ij}(n) = A_{ij}^n \]

Chapman-Kolmogorov Equation

\[ P_{ij}^{t+s} = \sum_{k=1}^{K} P_{ik}^t P_{kj}^s \] \[ A(t+s) = A(t)A(s) \]

State Probabilities Over Time

\(\pi(t)\) is the probability of being in state \(i\) at time \(t\) from the initial distribution: \[ \pi(t) = P(X_t = i) = \sum_{j=1}^{K} P(X_t = i \mid X_{t-1} = j) P(X_{t-1} = j) = P_{ij} \pi(t-1) \] \[ \pi(t) = \pi A^{t-1} \]

Hidden Markov Models

Basic Markov Models are very restrictive/simple and do not capture the complexity of the real world.

Probabilistic latent variable models for a sequence of observations: \(X_1 \rightarrow X_2 \rightarrow X_3 \rightarrow ... \rightarrow X_t\)

We use discrete time steps, while observations can be continuous or discrete.

Examples: - \(X_t\): location of a moving object - \(X_t\): word in a sentence

In many applications, the Markov property is not realistic as we have long dependencies. \(X_t\) does not capture all relevant information.

In many applications, the state is not directly known but can only be observed indirectly with sensor data. Markov Chain is a fully observed model - not realistic.

Example: Tracking a plane - Not observed/latent state \(Z_t\): physical vector quantities (position, velocity, acceleration) - \(X_t\): observed noisy measurements of the state (radar, GPS, etc.) - \(Z_t\) has the Markov property; one can approximate the state of the plane at time \(t\) given the state at time \(t-1\) - \(X_t\) doesn’t have to have the Markov property

Definition

A sequence of latent states \(Z_1, Z_2, ..., Z_t\) and observations \(X_1, X_2, ..., X_t\) where: - \(Z_t\) is a Markov chain - \(X_t\) is conditionally independent of all other states given \(Z_t\) - \(P(X_t | Z_1, Z_2, ..., Z_t, X_1, X_2, ..., X_{t-1}) = P(X_t | Z_t)\) - Distribution of \(X_t\) depends only on the current state \(Z_t\) - We assume discrete time and discrete latent states \(Z_t\) -> we can treat it as a Markov chain with a transition matrix \(A\) - \(X_t\) can be continuous or discrete

\[P(X_1, X_2, ..., X_t, Z_1, Z_2, ..., Z_t) = P(Z_1)P(X_1 | Z_1)P(Z_2 | Z_1)P(X_2 | Z_2) ... P(Z_t | Z_{t-1})P(X_t | Z_t)\]

HMM Diagram

• \(P(Z_1 = i) = \pi_i\)

• \(P(Z_t = j | Z_{t-1} = i) = A_{ij}^{t+1}\)

• \(P(X_t = j | Z_t = i) = B_{ji}^{t+1}\)

• \(A\) is \(K \times K\)

• \(B\) is \(K \times M\) where \(M\) is the number of observed states

• Too many parameters, we assume time homogeneous model

Tasks

1. Parameter estimation: Observed \(X_1, X_2, ..., X_t\) -> estimate \(\pi, A, B\) and the most likely sequence of states \(Z_1, Z_2, ..., Z_t\)

2. Inference:

   • Filtering: Infer \(Z_t\) given \(X_1, X_2, ..., X_t\) (online) - predict the location of a robot
   • Smoothing: Infer \(Z_t\) given \(X_1, X_2, ..., X_T\) (offline) given all observations - predict the stem of a word in a sentence
   • MAP inference: Infer the most likely sequence of states given the observations
     • \(\arg\max_z P(Z_1, Z_2, ..., Z_t | X_1, X_2, ..., X_t)\)
     • Mode of the posterior distribution
     • Viterbi decoding
   • Attention: Most probable sequence might be different than using smoothing per each time step

Filtering: Forward Algorithm

\[P(Z_t | X_1, X_2, ..., X_t) = \frac{P(X_1, X_2, ..., X_t, Z_t)}{P(X_1, X_2, ..., X_t)} = \frac{P(X_1, ..., X_t, Z_t)}{\sum_{Z_t} P(X_1, X_2, ..., X_t, Z_t)}\]

\(\alpha_t(i) = P(X_1, X_2, ..., X_t, Z_t = i)\) Vector of size \(K\)

\[P(Z_t | X_1, X_2, ..., X_t) = \frac{\alpha_t(i)}{\sum_i \alpha_t(i)}\]

Efficient computation of \(\alpha_t(i)\): - Recursive - \(\alpha_1(i) = P(X_1, Z_1 = i) = P(Z_1 = i)P(X_1 | Z_1 = i) = \pi_i B_{ix_1}\) - \(\alpha_{t+1}(k) = P(X_1, X_2, ..., X_{t+1}, Z_{t+1} = k)\) \(= P(X_{t+1}|X_{1:t}, Z_{t+1} = k)P(X_{1:t}, Z_{t+1} = k)\) \(= P(X_{t+1}|Z_{t+1} = k) \sum P(Z_{t+1} = k, Z_t = i, X_{1:t})\) \(= P(X_{t+1}|Z_{t+1} = k) \sum P(Z_{t+1} = k | Z_t = i)P(Z_t = i, X_{1:t})\) \(= B_{kx_{t+1}} \sum A_{ij} \alpha_t(i)\)

\(\alpha_{t+1} = B_{x_{t+1}} \cdot (A^T \alpha_t)\) \(O(K^2T)\) which is linear in \(T\)

The Forward-Backward Algorithm: Smoothing

We have seen the entire data sequence \(X_1, X_2, ..., X_T\) \[P(Z_t | X_{1:T}) = \frac{P(X_{1:T}, Z_t)}{P(X_{1:T})} = \frac{P(X_{1:t}, Z_t = k) P(X_{t+1:T}| Z_t = k)}{\sum_{Z_t} P(X_{1:T}, Z_t)}\]

\(\beta_t(i) = P(X_{t+1:T} | Z_t = i)\) Hence \(P(Z_t | X_{1:T}) \propto \alpha_t(i) \beta_t(i)\) just normalized over \(i\)

Backward algorithm computes recursively: - \(\beta_T\) initialization - Given \(\beta_{t+1}\) compute \(\beta_t\) - \(\beta_T(i) = 1\) (has to be to work out, it doesn’t exist) - \(\beta_t(j) = P(X_{t+1:T} | Z_t = j) = \sum_i P(X_{t+1:T}, Z_{t+1} = i | Z_t = j)\) \(= \sum_i P(X_{t+1}, Z_{t+1} = i | Z_t = j)P(X_{t+2:T} | Z_{t+1} = i)\) \(= \sum_i P(Z_{t+1} = i | Z_t = j)P(X_{t+1} | Z_{t+1} = i)P(X_{t+2:T} | Z_{t+1} = i)\) \(= \sum_i A_{ji} B_{t+1}(i) \beta_{t+1}(j)\)

\(\beta_t = A (B_{x_{t+1}} \cdot \beta_{t+1})\)

\(O(K^2T)\) which is linear in \(T\)

Final Solution

• Compute prob of being in state \(k\) at time \(t\) online: We compute \(\alpha\)
• Compute prob of being in state \(k\) at time \(t\) offline: We compute \(\alpha\) and \(\beta\)

MAP Inference: Viterbi Decoding

\[\arg\max_z P(Z_1, Z_2, ..., Z_t | X_1, X_2, ..., X_t) = \arg\max_z P(X_1, X_2, ..., X_t, Z_1, Z_2, ..., Z_t)\] \[= \arg\max [\log P(Z_1)P(X_1| Z_1) + \sum \log P(Z_t | Z_{t-1}) + \log P(X_t | Z_t)]\]

Bipartite graph with weights: \(-\log P(X_t | Z_t) P(Z_t | Z_{t-1})\) Find the shortest path from the source to the sink

We have \(TK^2\) edges and \(TK\) nodes, so we can use Dijkstra’s algorithm to find it in \(O(TK^2 \log(TK))\)

Parameter Estimation: Learning \(\pi, A, B = \theta\)

Solve \(\max_\theta \sum \log P(X_1, X_2, ..., X_T | \theta)\) No analytical solution due to marginalization Use EM algorithm same as in GMM

GMM is a HMM without dependencies

EM Algorithm for HMM

E-step: Compute \(\alpha\) and \(\beta\) - Evaluate the posterior \(P(Z|X, \theta_\text{old})\)

M-step: Update \(\pi, A, B\) - Maximize the expected joined log likelihood \(P(X, Z | \theta)\) under \(\theta_\text{old}\) - \(\theta_\text{new} = \arg\max_\theta \sum P(Z|X, \theta_\text{old}) \log P(X, Z | \theta)\)

The M-step is equivalent to maximizing the Evidence Lower Bound (ELBO) as in variational inference, which is a lower bound on \(P(X|\theta)\) - We are testing all possible \(Z\)s weighted by the probability of the \(Z\)s

The MLE estimate for parameters is just the expected counts of the transitions and the emissions and the initial state distribution

Additions

Continuous Observations: Gaussian Emissions

\(P(X_t | Z_t = i) = \mathcal{N}(X_t | \mu_i, \sigma_i I)\) It can be used for time series segmentation - \(Z_i\) are clusters of similar behavior - Observations are Gaussians coming from the clusters - Time series emits from one cluster until it switches to another cluster

It is the same as before; we use Viterbi decoding to find the most likely sequence of states

If we had continuous latent states and continuous observations, we could use Kalman filters

Extensions: Neural Hidden MM/Deep State Space Models

\(P(Z_t | Z_{t-1}) = \mathcal{N}(Z_t | f(Z_{t-1}), \sigma_z)\) \(P(X_t | Z_t) = \mathcal{N}(X_t | g(Z_t), \sigma_x)\) There are no constraints on \(f\) and \(g\) They can be NN optimized by gradient descent - in the M-step to get new \(\theta\) - Before we had closed-form solutions We don’t have to use Gaussian distributions

Discussion

We only discuss discrete time steps - it’s essentially just an ordered series In applications: - Asynchronous time - events/measurements can happen with different gaps - speech recognition, temporal point processes - Continuous time - measurements almost continuously, examples: temperature - continuous stochastic processes

Neural Networks

Modern approaches to handling sequential data are increasingly based on neural networks. In this section, we will discuss some of the most popular neural network architectures for sequential data.

Word Vectors

We aim to represent words as vectors.

One-Hot Encoding

One-hot encoding is a simple method but has significant limitations: - There is no relationship between the vectors of different words. - The approach does not scale well with the vast number of words and their forms.

Distributional Hypothesis

According to the distributional hypothesis, words that appear in similar contexts tend to have similar meanings. This means that: - Similar words have vectors near each other. - For example, “hotel” and “motel” can be interchangeable. - However, polysemy can cause issues; for instance, “duck” as an animal and “duck” as a verb would have the same vector despite different meanings.

Illustration: - “king” + “woman” = “queen”

Co-Occurrence Matrix

A co-occurrence matrix captures how often words appear together within a window of size \(l\) around \(x_i\): \(\{x_{i-l}, x_{i-l+1}, \ldots, x_{i+l}\}\). - The co-occurrence matrix \(M\) is of size \(V \times V\) and is typically sparse. - It remains high-dimensional, so dimensionality reduction techniques are often applied. - The matrix is usually normalized by the frequency of the words.

Word2Vec

Word2Vec offers a different way to generate word vectors, as introduced by Mikolov et al. in 2013.

Continuous Bag of Words (CBOW)

• Predicts the target word given context words.
• Not effective for rare words.

Skip-gram

• Predicts context words given a target word.
• Slower to train but can perform better for rare words and small datasets.
• Input: one-hot encoded word vector of size \(N\).
• Embedding: projects into a \(D\)-dimensional space.
• The \(i\)-th row of the embedding matrix (\(N \times D\)) provides the word vector.
• A matrix \(W\) of size \(D \times N\) is used to get the surrounding words.
• Model parameters: \(U\) and \(V\).
• Objective: maximize \(E(P(C|w, U, V))\), where \(C\) is the context word and \(w\) is the target word.
• \(P(C|w, U, V) = \prod P(C_i|w, U, V)\), and \(P(C_i|w, U, V) = \text{softmax}(w_i^T \cdot U \cdot V)_i\).
• \(U\) and \(V\) can be chosen to be the same.
• This results in a dot product between the target word and the context word.
• \(u\) is the embedding.

Training

• Each forward pass computes normalized probabilities over all words, which is inefficient for large vocabularies.
• Alternative: negative sampling.
  • Transforms the problem into a binary classification task.
  • Samples \(k\) negative words and one positive word.
  • Objective: maximize the probability of the positive word and minimize the probability of the negative words.
  • Uses sigmoid instead of softmax.

Note: This method ignores the order of words.

Recurrent Neural Networks (RNNs)

In word embeddings, we learn representations for individual words. To process a sequence of words with variable length, RNNs use word embeddings as input and process the sequence one word at a time.

Weight Sharing

• RNNs share weights across all time steps.
• Multiple layers of RNNs can be stacked on top of each other.

Definitions

Given a sequence of words \(x_1, x_2, \ldots, x_t\) and outputs \(y_1, y_2, \ldots, y_t\), we want to compute the probability \(P(y_i | x_1, x_2, \ldots, x_i)\). - A sequence \(x_1\) to \(x_{t-1}\) is represented by a hidden state \(h_{t-1}\). - The network takes \(h_{t-1}\) and \(x_t\) to produce \(h_t\), from which we predict \(y_t\).

Equations: \[ z_t = W_h h_{t-1} + W_x x_t + b \] \[ h_t = \tanh(z_t) \] \[ o_t = V h_t + c \] \[ y_t = \text{softmax}(o_t) \]

The network is fully differentiable, allowing backpropagation through time (BPTT).

Loss: \[ L = - \sum \log P(y_i | x_1, x_2, \ldots, x_i) \]

Backpropagation Through Time (BPTT)

\[ \frac{\partial L}{\partial V} = \sum (y_t - \hat{y}_t) h_t^T \] Since parameters are shared, the final derivative is a sum of all contributions: \[ \frac{\partial L}{\partial h_t} \text{ is a function of } h_{t+1} \text{ and depends on the future.} \] \[ \frac{\partial L}{\partial h_t} = \sum_{s=t}^N \frac{\partial L}{\partial h_s} \frac{\partial h_s}{\partial h_t} = \sum \ldots \prod W \] - If \(W\) has eigenvalues larger than 1, the gradient will explode; if smaller than 1, it will vanish. - RNNs struggle to retain information for long sequences.

Gated Recurrent Unit (GRU)

GRUs modify the architecture to retain information longer by using a gating mechanism.

Equations: \[ z_t = \sigma(W_z[h_{t-1}, x_t]) \] \[ r_t = \sigma(W_r[h_{t-1}, x_t]) \] \[ \hat{h}_t = \tanh(W_h[r_t \odot h_{t-1}, x_t]) \] \[ h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \hat{h}_t \]

• If \(r_t = 0\), the previous state is ignored.
• If \(z_t = 0\), the new state is ignored.
• The gates mix the previous and new states as needed.

Long Short-Term Memory (LSTM)

LSTMs, invented by Hochreiter and Schmidhuber in 1997, use three gates: input, forget, and output.

Equations: \[ i_t = \sigma(W_i[h_{t-1}, x_t]) \] \[ f_t = \sigma(W_f[h_{t-1}, x_t]) \] \[ o_t = \sigma(W_o[h_{t-1}, x_t]) \] \[ \tilde{c}_t = \tanh(W_c[h_{t-1}, x_t]) \] \[ c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t \] \[ h_t = o_t \odot \tanh(c_t) \]

LSTMs maintain both short-term (cell state) and long-term (hidden state) memories. This structure allows for better gradient flow and alleviates the vanishing gradient problem, although training can still be challenging.

Non-Recurrent Models (ConvNets and Transformers)

Sometimes, the full history of a sequence is not needed. Recall autoregressive models, which use a fixed window of the past. While RNNs share parameters across all time steps and depend on the full history, non-recurrent models provide alternative approaches.

Convolutional Neural Networks (ConvNets)

ConvNets can process sequences using convolutions.

• In 2D, convolutions use a filter that slides over the image.
• For sequences, we use 1D convolutions.
• WaveNet, for example, uses dilated convolutions to increase the receptive field, adding gaps between the filter elements to ensure causality. This ensures that the output at time \(t\) only depends on the past.

ConvNets are easier to train and parallelize, with predictions at each time step happening in parallel.

Transformers

Transformers use learned weighting of each element in the sequence instead of fixed weighting, as in convolutions.

Cross-Attention

Inputs: - \(X\): The query, representing the English sentence to be translated. - \(X'\): Both the key and value, representing the German sentence.

Mechanism: - The attention mechanism identifies important parts of \(X'\) (German sentence) for translating \(X\) (English sentence).

Attention Calculation: 1. Deriving Queries, Keys, and Values: - Queries (\(Q\)) are derived from \(X\) (English sentence). - Keys (\(K\)) and Values (\(V\)) are derived from \(X'\) (German sentence).

2. Calculating Attention Scores:
   • Attention scores are the dot product of queries (\(Q\)) with the transpose of keys (\(K^T\)).
   • Scores are scaled by the square root of the dimensionality of the keys (\(d_k\)) for stability.
   • Softmax is applied to these scaled scores to obtain attention weights: \[ \text{Attention Weights} = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) \]
3. Computing the Weighted Sum:
   • Attention weights compute a weighted sum of the values (\(V\)), resulting in the final attention output (\(z\)): \[ z = \text{Attention Weights} \times V \]

Result: - The output \(z\) is an updated representation of \(X\) (English sentence) incorporating relevant information from \(X'\) (German sentence).

Self-Attention

• \(X\) and \(X'\) are the same.
• Self-attention examines relationships between words within the same sentence, acting as a generalized convolution with a data-dependent kernel for the entire sequence.

Positional Encoding

• Attention mechanisms are permutation equivariant, meaning they do not inherently capture word order.
• Positional encoding, often a Fourier transform of the position, addresses this limitation by adding position information to the embeddings.

Multi-Head Attention and Complexity

• Multi-head attention combines the output of \(h\) self-attention heads.
• Each head has its parameters, and their outputs are concatenated and linearly transformed to reduce dimensionality.
• Each head computes \(n^2\) attention scores, making this approach intractable for long sequences.
• Solutions include fixing the structure of attention weights, low-rank approximations, and downsampling the sequence length.

Structured State Space Models (S4)

State Space Model Basics

A discrete-time state space model is defined by the following equations:

\[ \begin{aligned} x_{k+1} &= \mathbf{A}x_k + \mathbf{B}u_k \\ y_k &= \mathbf{C}x_k + \mathbf{D}u_k \end{aligned} \]

Where: - \(x_k \in \mathbb{R}^N\) is the state vector - \(u_k \in \mathbb{R}\) is the input - \(y_k \in \mathbb{R}\) is the output - \(\mathbf{A} \in \mathbb{R}^{N \times N}\), \(\mathbf{B} \in \mathbb{R}^N\), \(\mathbf{C} \in \mathbb{R}^{1 \times N}\), \(\mathbf{D} \in \mathbb{R}\) are the model parameters

Recurrence as a Convolution

By recursively applying the state equation, we can express the output as a convolution:

\[ \begin{aligned} x_0 &= \mathbf{B}u_0 \\ x_1 &= \mathbf{A}\mathbf{B}u_0 + \mathbf{B}u_1 \\ y_k &= \mathbf{C}\mathbf{A}^k\mathbf{B}u_0 + \mathbf{C}\mathbf{A}^{k-1}\mathbf{B}u_1 + \cdots + \mathbf{C}\mathbf{B}u_{k-1} \end{aligned} \]

This is equivalent to a convolution with a sequence-length kernel:

\[y = K * u, \text{ where } K = [\mathbf{C}\mathbf{B}, \mathbf{C}\mathbf{A}\mathbf{B}, \mathbf{C}\mathbf{A}^2\mathbf{B}, \ldots]\]

Convolution Equivalence

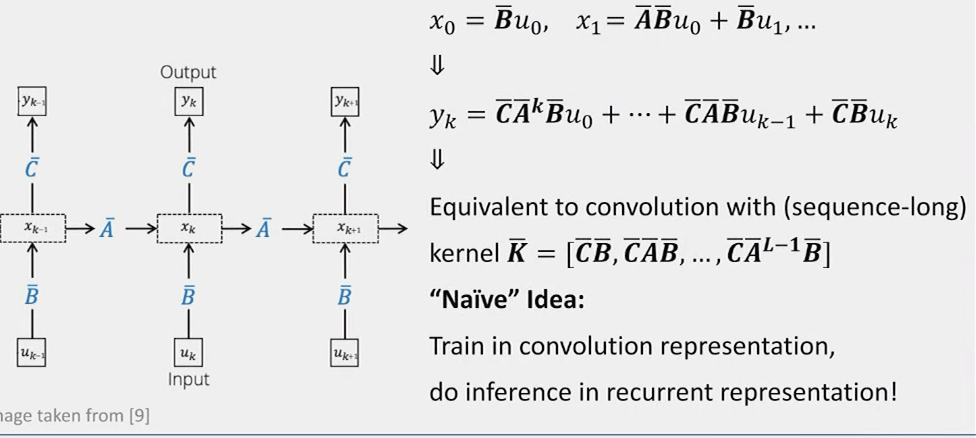
Computational Complexity

The naive implementation has a complexity of \(O(N^2L)\) for a sequence of length \(L\), which is impractical for long sequences.

Efficient Computation

To reduce complexity, we can diagonalize \(\mathbf{A}\):

\[\mathbf{A} = \mathbf{V}\boldsymbol{\Lambda}\mathbf{V}^{-1}\]

Continuous Time View and HIPPO Initialization

To address the vanishing/exploding gradient problem, we can use a continuous-time perspective:

\[\frac{d}{dt}x(t) = \hat{\mathbf{A}}x(t) + \hat{\mathbf{B}}u(t)\]

The discrete-time \(\mathbf{A}\) is related to the continuous-time \(\hat{\mathbf{A}}\) by:

\[\mathbf{A} = e^{\Delta \hat{\mathbf{A}}}\]

Where \(\Delta\) is the step size.

Continuous Time View

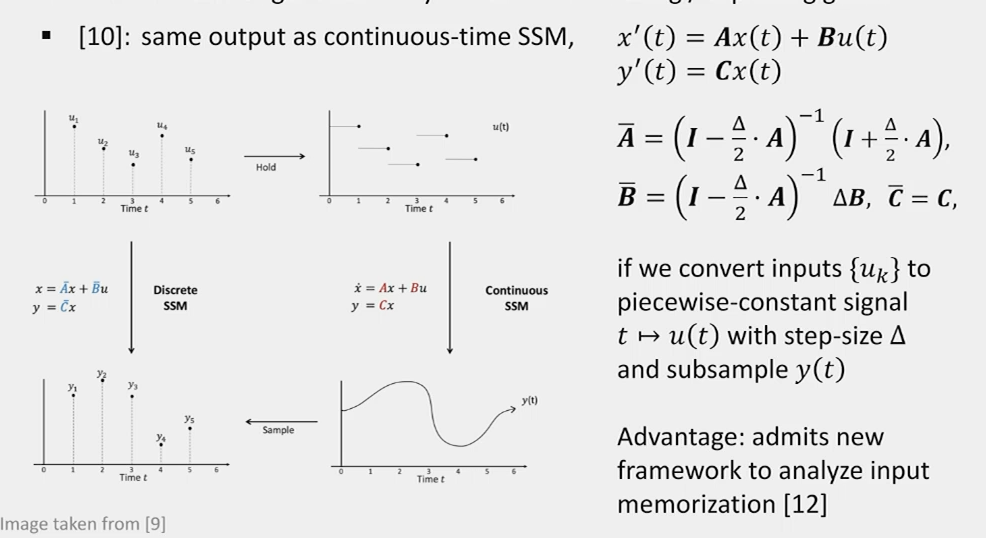
The HIPPO (HIerarchical Positive Orthogonal) initialization sets \(\hat{\mathbf{A}}\) to a specific form that ensures stable gradient flow and long-term memory. It’s based on the recurrence relation of Legendre polynomials.

Legendre Polynomials (LP)

The nth Legendre polynomial \(P_n(x)\) satisfies:

\[(2n+1)xP_n(x) = (n+1)P_{n+1}(x) + nP_{n-1}(x)\]

This recurrence relation allows efficient updates of the state as new data points are added.

S4: Structured State Space for Sequences

The S4 model combines these elements:

1. HIPPO initialization of \(\hat{\mathbf{A}}\)
2. Efficient kernel computation using the diagonalization trick
3. Multiple layers with non-linearities (e.g., ReLU) between them
4. Residual connections: \(y^{(l)} = u^{(l)} + \text{S4}(u^{(l)})\)

The full S4 layer can be expressed as:

\[\text{S4}(u) = \phi(K * u + b)\]

Where \(\phi\) is a non-linearity and \(b\) is a bias term.

S4 has achieved state-of-the-art performance on various long-range sequence modeling tasks, outperforming traditional RNNs and even Transformers in some cases.

Temporal Point Processes

Introduction

The main difference is that now the exact time is important, not just the ordering of events.

• Time series: Measurements at regular intervals
• Temporal point processes: Asynchronous time with events at irregular intervals

Key Characteristics:

• Distribution over time points
• Discrete event sequence in continuous time
• Both location and time are random

We can model it autoregressively:

• Predict the time of the next event given the history \(H_t = \{ t_j \mid t_j < t \}\)
• \(H_t\) depends on a specific sample \(\{ t_j, t_n \}\)
• We denote the conditional density \(p^*(t) = p(t \mid H_t)\)
• The next event in \([t, t + dt]\) is \(p^*(t) \, dt\) and there is no event before \(t\)

Conditional Density:

• Cumulative distribution function (CDF): \[ F^*(t) = \int_{t-1}^t p^*(t) \, dt \] Probability that the next event is between \(t-1\) and \(t\)

• Survival function: \[ S(t) = 1 - F^*(t) = \int_t^\infty p^*(t) \, dt \] Probability that the next event is after \(t\)

• Conditional intensity function: \[ \lambda(t) = \frac{p^*(t) \, dt}{S^*(t)} = \frac{P(\text{event in } [t, t + dt] \text{ and no event in } [t-1, t])}{P(\text{no event in } [t-1, t])} \] Probability of the next event in \([t, t + dt]\) given that there is no event in \([t-1, t]\)

  • Intuitive interpretation: Number of expected events per unit of time
  • Not a probability

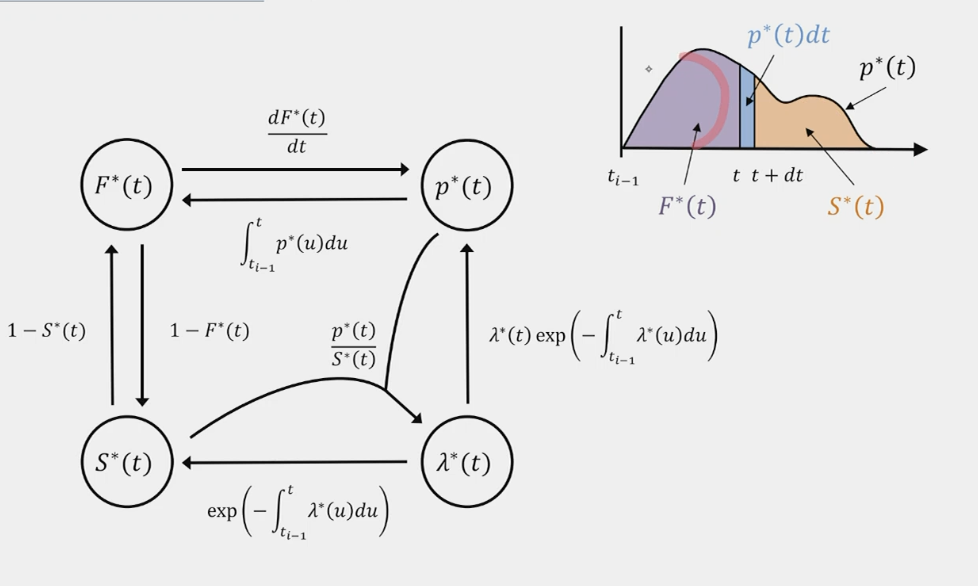
The likelihood of the entire sequence with \(t_1, t_2, \ldots, t_n\) events on \([0, T]\) is:

\[ p(t_1, t_2, \ldots, t_n) = p^*(t_1) \cdot p^*(t_2) \cdots p^*(t_n) S^*(T) = \lambda(t_1) \lambda(t_2) \cdots \lambda(t_n) \exp \left( - \int_0^T \lambda^*(t) \, dt \right) \]

\[ p^*(t_1) = \lambda(t_1) \exp \left( - \int_0^{t_1} \lambda^*(t) \, dt \right) \]

Challenges:

• We don’t like the integral
• The number of events can vary

Models Based on Conditional Intensity Functions

• More flexible and interpretable
• Easy to combine different TPPs with different \(\lambda^*(t)\) to produce a new TPP
• Efficient sampling

Homogeneous Poisson Process (HPP)

• Simplest possible model
• \(\lambda^*(t) = \mu\)
• \(p^*(t) = \mu \exp(-\mu (t - t_1))\) is an exponential distribution

We can interpret it as modeling the inter-event times that are exponentially distributed.

Sampling:

• Generate an exponential random variable with rate \(\mu\) and add it to the last event time
• It doesn’t depend on the history (memoryless property), so we can sample all events at once

Inhomogeneous Poisson Process (IPP)

• Intensity function is time-dependent: \(\lambda^*(t) = \mu(t) \geq 0\)
• Still doesn’t depend on the history (memoryless property)
• Captures global trends (e.g., cars on the road during rush hour)

Expected Number of Events:

\[ N([a, b]) \sim \text{Poisson} \left( \int_a^b \mu^*(t) \, dt \right) \]

Simulating an IPP:

• Simulating inter-event times is hard and requires integration
• Better alternative: Thinning algorithm
  • Find the upper bound of the intensity function \(\lambda^*(t) \geq \max_t \mu(t)\)
  • Sample a time \(t\) from an HPP with rate \(\lambda^*\)
  • Accept \(t\) with probability \(\mu(t) / \lambda^*\)
  • Essentially acceptance-rejection sampling

Hawkes Process

• Self-exciting process
• Example: Tweets, where one tweet triggers another, then a pause until another tweet

\[ \lambda(t) = \mu + \alpha \sum_i k_w(t - t_i) \quad \text{where } t_i < t \]

• Triggering kernel: \(k_w(t - t_i) = \beta \exp(-\beta (t - t_i)) \text{ for } t > t_i\)
• Parameters: \(\mu, \alpha, \beta\)
• Depends on the history
• Exhibits clustered, bursty behavior

Parameter Estimation in TPPs

• Maximize the likelihood of the observed data over the parameters (iid learning setting)

\[ \log P(t_1, t_2, \ldots, t_n) = \sum_i \log \lambda^*(t_i) - \int_0^T \lambda^*(t) \, dt \]

• Various optimization algorithms
• Simple models like HPP allow for closed-form solutions
• For Hawkes, we can use convex optimization
• We can use gradient descent with modifications for constraints

Advantages and Disadvantages of Using Intensity:

• Numerical integration might be intractable
• Not clear how to define flexible models with arbitrary dynamics
• Easy to interpret, sample, and define models with simple dynamics

We will revisit RNNs with conditional probability.

Directly Model the Conditional Density \(p^*(t \mid H_t)\) with an RNN:

• Every time an event happens, we feed \(\tau_i = t_i - t_{i-1}\) to the RNN
• Use the hidden state to model the history
• Use it to model the parameters of the \(p^*\) distribution
• \(p^*_t = p(t \mid H_t) = p(t \mid h_i)\)

How to Model \(p^*\):

• Simple non-negative distributions: Exponential, Gamma, Weibull, Gompertz
• Use a mixture of distributions: Convex combinations of densities
• If we pick the exponential distribution, it’s not an HPP nor an IPP since it depends on the history and the parameter \(\mu\) changes over time

Normalizing Flows:

• Use transformations like \(\exp(\log(1 + \exp))\) to ensure that the output is positive, combine with other transformations to get a flexible distribution

Problems with Autoregressive TPPs:

• Error accumulation
• Computational complexity
• Hard to model long-range interactions

Alternative: ADD and THIN - Diffusion for TPPs

• Noising: Data sample \(t_0 \sim \lambda_0\)
• For every diffusion step \(n\):
  • Thin \(t_{n-1}\) = randomly remove events from data
  • Add events from HPP superposed with the history
• End up with completely noised data according to the HPP
• End: Noised data \(\tilde{t}_n \sim \lambda_{\text{HPP}}\)
• Learn the denoising process
• Now we take the entire sequence into account, not autoregressive

Marked TPPs

• Most common type: Categorical mark (type of tweet)
• Each event has a category
• Events of different classes can influence each other
• We can have a distribution over the types: The hidden state can be used to model the type represented by a categorical distribution